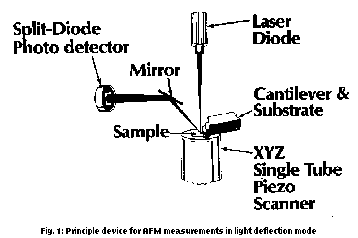
Atomic force microscopy AFM (or SFM) was developed in 1986 by Binnig, Quate and Gerber [1]. Contrary to STM which is already widely available, it enables also the investigation of non-conducting surfaces, because it scans van der Waal's forces with "atomic" tips. This opens a new world of submicroscopic methods of investigation. After the Nobel prize award in 1986 to Binnig and Rohrer for the discovery of STM also AFM developed rapidly. Several vendors are on the market with commercial instruments since 1990/91. The instruments of most manufacturers provide high comfort and rich imaging facilities. In view of unusually versatile applications which are possible it appears that the only obstacles for broader use of AFM are only the present financial difficulties in the funding of science. AFM (and STM) offer lateral and vertical resolutions up to the atomic scale and three-dimensional representations, which cannot be met by any other techniques.
The new technique of measurement was needed, because numerous questions concerning chemical reactions of organic crystals with light or with gases urgently waited for elucidations. Gas/solid reactions were unexpected (i.e. genuinely new) and unintelligibly effective. The reasons for their unexpected success remained puzzling worldwide. As ever, the genuine scientific novelty meant that one had breath-taking new results prior to the theoretical background. Therefore we had to probe the new technique systematically on the chemically reacting crystals and this led to the previously not thinkable understanding [2]. In the same way AFM opened new ways for clarifying urgent questions with crystal photolyses [3], which will be dealt with in this article.
In the atomic force microscopy solid surfaces (this includes also molecular mono- or double-layers of tensides on solid supports, so-called Langmuir-Blodgett- or LB-films) are scanned with respect to constant van der Waals forces in the region of 10-9 to 10-6 N force point by point, line by line and processed to a surface image with the aid of a computer. This is achieved by the setup of Fig. 1, which shows the most used measuring device (also the one of the most frequently used Nano-Scope II/III). The standard tip (on sale, measuring tip with "atomic" end) is epitactically grown Si3N4 or Si on a cantilever (with a very low spring constant of e.g. 0.1 Nm-1) in the form of a pyramide (in the case of Si3N4 vertex angle of 45°). It points downward toward the sample. The cantilever is tilted by some degrees and fastly connected to the measuring head over the substrate. It is hit by a focussed laser beam on its gold coated backside from the tip. There is reflection into a split-diode photo-detector over a mirror. After the fixing of the force a XYZ piezo drive scans usually 400 x 400 raster points. The data are collected separately in XY- and Z-direction in order to allow height adjustment and magnification in Z-direction separately. If the tip hits an elevation or a deepening on the sample, the cantilever will be bent, the laser beam deflected. This will be fed back to the piezo control and immediately balanced by a height correction. The signal which is gained by that will be saved for any raster point. The entirety of the points is the surface image.

This technique is very sensitive especially in Z-direction. Also the XY-area can be diminished so strongly by the piezo drive, that as in the case of STM individual atoms may be resolved. For more mobile organic and biological materials at present the limit is more at the molecular resolution. This epoch-making goal which has been reached in several instances without doubt [4] is by far not the whole story. Rather there is a high need for representations of 10 to 15000 nm width and even larger (e.g. with data supports, ceramics, foils). This is also particularly valid for chemically reacting surfaces. Contrary to light microscopy there are no problems with depth of focus. One obtains always 3D-images with enormous richness in details, which may be measured precisely in terms of heights (up to 5µ), distances, angles. Standard tips with the vertex angles of 45° can at most measure slopes up to this angle (1:1-images) (at steeper slopes one observes characteristic tip-artifacts which may be avoided with needle type special tips or tapping and non-contact mode measurements), however, steeper objects are rare on organic surfaces.
The adequate representation of AFM-results are parsimoniously and without loss of information digitally filtered planefitted (best basic plane) perspective images which are usually illuminated sideways. For the measurement of distances, angles, roughness one may use any projections, cuts, and histograms in any commercial imaging software, it appears. A real breakthrough in the imaging was the creation of the possibility to digitally illuminate from any direction above the mean plane with adjustable light intensity and mix in of an adjustable portion of colour height coding (at Digital Instruments from NanoScope III). With that the previous shadows may be diminished such that phantastic image qualities can be achieved, which could not be reached with illumination from one of five directions. In particular all details can be imaged more clearly.
Solid state photolyses become more and more important for imaging and information storage. It has been known for a long time that photoreactions in the crystal depend on the crystal lattice and it does not need to be explained, that it will be favourable if all reacting atomic centers are arranged in close proximity. However, Schmidt formulated his "topochemical postulate" in several papers, whereupon any reacting double bonds must be at most 4.2 Å distant and parallel in the crystal and very obviously the dimer structure (stereochemistry) will be determined by the crystal lattice. This was found in numerous experiments [5], however, there are remarkable exceptions which show that this does not reach too far and cannot be the whole truth [3, 5]. In particular it was quite clear from the beginning, that in almost any case the crystal lattices will change upon photoreaction (no topotacticity). There are definitely photostable crystals with parallel double bonds which are less distant than 4.2 Å and there are photoreactive crystals with considerably higher double bond distances (e.g. 4.8 Å, in mixed crystals also 7.8-9.8 Å [5] or large angles between the double bonds (e.g. 65° but also 135° in 2,5-dibenzylidene-cyclopentanone [5,6]). Even dimer structures which directly contradict the crystal structure and have thus been bewildering topochemists for decades occur (very well known example: 9-cyanoanthracene). All crystallographic auxiliary hypotheses were not convincing. Finally there were found crystals which formed several isomeric photodimers [6] which put new puzzles to the topochemical postulate. Here again, AFM is challenged for new insights [3].
The AFM-measurements used a NanoScope II of Digital Instruments, Santa Barbara, with Si3N4-standard tips at room temperature in air. Any photooxidations were excluded by AFM-scans of crystals which had been irradiated under vacuum shortly before admission of ambient conditions: In any case they showed similar features on the surfaces. The crystals were glued to the scanner as flatly as possible (< 10°). After an initial scan the head was removed and the crystal irradiated directly on the scanner from 5 cm distance with a water-cooled high pressure mercury lamp (Hanau 150 W) through a Solidex filter. After replacing the head the initial area of the crystal was routinely found again without difficulties within a few hundreds of nm (Fig. 2), provided the crystal had not cracked.
A planefit calculation fixed the basic plane horizontally and statistical noise on the individual images was eliminated without loss of information by flattening and parsimonious low-pass filtering. The scan range was chosen as wide as possible initially (15000 nm) in order to secure uniform features all over (in further scans also at different areas of the same face on the same or new crystals). Then the scan range was reduced for best appearance of the features formed. For the same purpose the enlargement in Z-direction is optimized in any case. The image processing was done by using the NanoScope III system, the video prints created with a Mitsubishi videoprinter CP-200E (H). The axes and subdivision with plain figures (as in NanoScope II and now also with the NanoScope III) had to be drawn by hand, photographed and precisely mounted to the printing pattern. The crystal lattice diagrams were calculated and plotted from the known X-ray crystal data by using the program SCHAKAL 92 (AIX-UNIX version, E. Keller, Universität Freiburg) on an IBM RS6000 32H workstation. Van der Waals surfaces have been calculated semiempirically with the program MOPAC (PM3) of QCPE on the vector computer Convex and imaged by use of PCMODEL (QCPE).

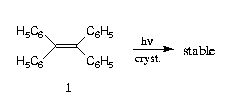
The generally accepted standard for topochemical behaviour are the photodimerizations of the alpha- and ß-modifications of trans-cinnamic acid 2 to give alpha-truxillic acid 3 and ß-truxinic acid 4, resp. Thereby it is supposed that the reactions occur in the interior of the crystals in a so-called "reaction cavity". For the newly formed product crystals there is allegedly said that there be "complete absence of orientation" (the frequently cited X-ray recordings which seem to "substantiate" this claim could be taken only in a very late stage of the reaction: see Ref. [3]). However, an examination of the literature shows, that regularly it was irradiated in a way that the incident light was absorbed by the first 300 molecular layers under the surface whenever 3 or 4 were synthesized.

Figure 3 shows the photochemical result for the alpha-modification of 2 on the morphologically very dominant (010)-face. Prior to irradiation there are many terraces (30 Å high, the sporadic hills are probably hydrates of 2). After short irradiation one sees epitactically grown planes and parallel furrows (1600-3200 nm distant) which lie transversal to the c-axis. Evidently, an increase in density has to be compensated for. At right angles to the furrows there slide up floes with layered structure vertical to the a/c-plane, as can be seen in the zoomed image 3c. Upon prolongued irradiation these floes grow out to overlapping plates (see Ref. [3]). The depth of the furrows corresponds to the initial penetration depth of the light.
We see that there are very complex material transports which accompany the reaction in the surface region and that there are kept well defined orientations in contrast to previous claims and theories. This holds as long as the light which will penetrate further and further into the crystal through the now transparent surface region does not finally burst the crystal upon further progressing reaction.
It is now possible to interpret on a molecular basis if we compare the molecular packing of alpha-2 and the molecular shapes of 2 and 3.which are semiempirically (PM3) calculated with high reliability.Figure 4 shows that the monomers in alpha- 2 cut the (010)-face under the flat angle of 30°. There is an accordion-like structure. The dimer 3 which is formed all over after light absorption can fit into the basic lattice if it turns in the ways indicated by the arrows.

This gives mixed crystals of 3 in alpha-2 which retain their molecular orientation as long as possible. The furrows form in confirmation of this interpretation along the weakly interacting zones between the layers, where there are no hydrogen bridges. Thus, the projection of the zig-zag staple on the a/c plane cuts the c-axis at an angle of 39° in good agreement with the angle of ca. 45° which had been visually estimated under the microscope [3]. The floes which slip over at right angles and continue to grow are the result of a thermal phase transformation if the mixed crystals become richer and richer in 3. Thus, finally there are formed mixed crystals of 2 in the lattice of 3 (Cc, a = 16.09, b = 5.67, c = 16.35, ß = 99.38°) because the number of hydrogen bridges will have to be maximized.
The ß-modification of 2 enables AFM-scans of the morphologically dominant (100)-face, but also on (010). Interestingly, the results are complementary (crater- and volcano-formations).
Short irradiation of the pretty flat (100)-plane of ß- 2 yields well-shaped craters (500 nm in diameter, 200 nm deep), as is shown in Figure 5b. In addition to that the folding up at the edges shows, that material has been lifted over the initial surface level.

Again there are enormous well directed material transports at the surface in the region down the light penetration depth. Interestingly, the craters disappear completely upon continuation of the irradiation and there is formation of a weakly currugated but again very flat surface (Fig. 5c). All of that could not be expected on the basis of the topochemical postulate and its refinements and auxiliary hypotheses. This must be understood in detail.
The molecular interpretation is far from being trivial. However, the complexity does not leave much choice. According to the crystal structure diagram in Figure 6 the molecules 2 stand on (100) almost vertically (83°) in horizontal layers. As usual, the crystal model was the isomorphous 4-chloro-trans-cinnamic acid, the very closely related lattice parameters of which are given in Figure 8, because an X-ray structure analysis of ß- 2 is still missing. From Figure 6 it is again recognized with the aid of the calculated molecular shapes that the dimer molecules 4 fit in almost ideally into the ß-2 lattice after the turns as indicated by the arrows. However, the measurement of 4 shows that it is by 30% slimmer than two monomers of 2. Therefore, there must be a shrinking upon formation of the mixed crystals. Due to the light intensity gradient this has to be faster at the surface than in the deeper layers which obtained less of the incident light. Thus, the crater formation is convincingly explained. The necessary growth upward in the vertical direction is understandable, because the hydrogen bridges of ß-2 which lie in this direction (Fig. 6) are broken up upon dimerization. At 30% linear shrinking the surface diminishes by at most 50% (calculated 49%). It may be judged (even better from projections of the image 5b) that we do have about that limiting value in Figure 5b and this is in support with this interpretation.
The disappearance of the craters upon continued irradiation again will have to be traced to a thermal phase transformation, because finally the crystal lattice of 4 with less and less embedded molecules 2 must be formed. It has been shown by hydration that there is still order on the surface of Figure 6c, because this reaction forms valleys and ridges according to AFM scans, while on the contrary a similarly treated (010) face of ß-2 gives craters at this point (cf. [3]).


The (010)-plane of ß-cinnamic acid to which the molecules grow on faster has a distinct floe structure similar to a pile of boards according to Figure 7a. Irradiation gives volcano-like hills initially and later on a weakly corrugated flat surface. However, this one (Fig. 7c) has a different molecular order than the one originating from (100) in Figure 5c, as has been shown by the above-mentioned hydration experiments. Again the clearly directed transport phenomena are in sharp contrast to previous suppositions. Again the features can be interpreted on the molecular level (Fig. 8): The molecules 2 lie very flat (23°) on (010). The dimer molecules 4 fit in the host lattice. This gives the above-mentioned shrinking by 30%. In order to compensate for that monomers 2 will have to slide in from all sides. Thus the volcanoes model themselves out because there is free space created all around (in other cases one will rather conclude, that volcanoes grow up over the initial surface level [2]). The final leveling will be again caused by a thermal phase transformation.
The very detailed molecular interpretations of the stereoselective [2+2]-dimerizations of the two trans-cinnamic acid modifications derive from the unexpected richness in details of the self-explanatory AFM-images. The clearcut proof of reactions in the surface region with complicated though well directed material transports over large distances shed new light on the many violations of the topochemical principle. The initial crystal arrangement undoubtedly creates an advantage for the corresponding stereochemistry in the products and thus establishes the usual improvements in stereoselectivity of crystal photolyses versus liquid ones. However, this does not constitute a dogma, because there are further effects that may effectively disfavour those geometries in other cases. It is quite true and self-evident that small distances will be advantageous for the chemical reaction. However, the photoprocesses are governed by the phase rebuildings predominantly, because the molecular transports which are observed experimentally are by far larger than the intermolecular distances of the reactants in the crystal (not all crystals with small distances are photoreactive!). This is shown in the Figures 3, 5, and 7 with high richness in details.
The AFM-technique is in a process of rapid development and does continuously invent new applications in chemistry, biology, materials' research (polymers, ultrathin layers and coverings, semiconductors, superconductors), tribology and in the creation of nanostructures (these at higher applied forces). There are, of course, (more expensive) versions of scanning microscopes that scan (if necessary under vacuum and at 77 K or at 4 K) not only van der Waals, but also magnetic, electrostatic, or lateral forces, electrochemical processes at electrode surfaces, and optical properties.
With simplest means and in a very short time we could observe a series of basic mechanisms for chemically enforced phase rebuildings on organic crystal surfaces and we could use this to reach hitherto not thinkable answers to long waiting intriguing mechanistic questions. Still any new application of AFM unravels unexpected novelties, so that there will be a great future ahead. At any rate AFM starts to become a routine technique that can do much more than just imaging individual atoms. A continuation of this subject in GIT, issue 7, 1993, will deal with topochemically allowed and forbidden [4+4]-photodimerizations.
We thank L.O.T., Darmstadt, for the contribution to the colour print costs, the provision of their facilities for the preparation of the colour print patterns, and for Figure 1. For the determination of the Miller indices we are indebted to Prof. W. Rammensee and Dr. J. Schreuer, Universitaet zu Koeln.
[1] BINNIG, G., QUATE, C. F., GERBER, CH.: Phys. Rev. Lett. 56, 930 - 933 (1986)
[2] KAUPP, G.: Mol. Cryst. Liq. Cryst. 211 (1992) 1 - 15 (1992)
[6] KAUPP, G., ZIMMERMANN, E.: Angew. Chem. Int. Ed. Engl. 20, 1018 - 1019 (1981)